统计学相关
协方差、协方差矩阵
标准差和方差一般是用来描述一维数据的,针对多维数据,协方差就是用来度量两个随机变量关系的统计量,仿照方差的定义
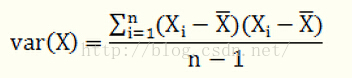
给出协方差的定义
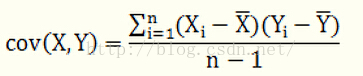
协方差的结果为正值,则表明两者是正相关的,结果为负,则说明两个变量之间的负相关,如果为0,则说明两者之间没有关系,也就是“相互独立”。
协方差只能处理二维问题,,随着维数的增加,需要计算多个协方差,所以需要用矩阵组织这些数据,写明是协方差矩阵的定义:
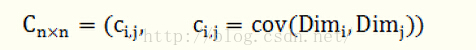
假设数据集有三个维度,则协方差矩阵为:
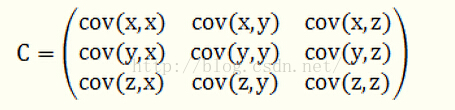
由上可知,协方差矩阵是一个对称矩阵,对角线为各个维度的方差。
相关系数、相关系数矩阵
相关系数是用来反映变量之间相关关系密切程度的统计指标,相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度,计算公式如下

相关系数的值介于–1与+1之间,即–1≤r≤+1。其性质如下:
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关。
- 当|r|=1时,表示两变量为完全线性相关,即为函数关系。
- 当r=0时,表示两变量间无线性相关关系(不是说两个变量之间完全不相关,应该是线性不相关)
- 当0<|r|<1时,表示两变量存在一定程度的线性相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
- 一般可按三级划分:|r|<0.4为低度线性相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关。
相关系数矩阵是由矩阵各列间的相关系数构成,相关矩阵第i行第j列的元素就是原矩阵第i列和第j列的相关系数。
总结:由协方差矩阵和相关矩阵的公式定义可知,经标准化(或正态化:将原始数据处理成均值为0,方差为1 的标准数据)的样本数据的协方差矩阵就是原始样本数据的相关矩阵。
附上pandas处理多维数据,一般用来查看标签变量的统计特性和相关性
|
|